Himpunan - Matematika Diskrit TI 16-B

A. Pengertian Himpunan

Himpunan adalah sekumpulan objek atau benda yang memiliki karakteristik yang sama atau
terdefinisi dengan jelas.
Contoh himpunan :
1. kumpulan nama hari dalam seminggu
2. kumpulan warna lampu lalu lintas
3. kumpulan makanan manis

contoh bukan himpunan :
1. kumpulan lukisan indah
2. kumpulan wanita cantik
3. kumpulan anak pintar

B. Notasi Himpunan dan Anggota Himpunan

Nama himpunan ditulis dengan huruf kapital dan anggotanya ditulis diantara kurung kurawal.

notasi 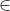 untuk menyatakan anggota himpunan

notasi 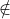untuk menyatakan bukan anggota himpunan

C. Cara Menyajikan Himpunan

1. Mendaftarkan anggotanya (enumerasi)

Contoh: = {3, 5, 7}

2. Menyatakan sifat yang dimiliki oleh anggotanya

Contoh: A = Himpunan semua bilangan ganjil yang lebih dari 1 dan kurang dari 8.

3. Menuliskan notasi pembentuk himpunan

Contoh: = {x |1 < x < 8, x adalah bilangan ganjil}

D. Bilangan Kardinal

Bilangan kardinal himpunan A adalah bilangan yang menyatakan banyak anggota himpunan A, ditulis n(A)

contoh : 

A= {a, i, u, e, o}, maka n (A) = 5

E. Macam-macam Himpunan

a. Himpunan Bilangan : bilangan asli, bilangan cacah, bilangan ganjil, bilangan genap, dan lain-lain

b. Himpunan kosong : Himpunan yang tidak memiliki anggota, ditulis    {  } 

c. Himpunan Terhingga : merupakan himpunan yang memiliki banyak anggota terbatas

d. Himpunan tak terhingga : merupakan himpunan yang memiliki banyak anggota tak terbatas

F. Himpunan Semesta

Himpunan semesta adalah himpunan seluruh unsur yang menjadi objek pembicaraan dan
dilambangkan dengan S.
Suatu himpunan dapat dinyatakan dengan cara menuliskan anggotanya dalam suatu gambar (diagram) yang disebut dengan diagram Venn

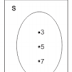
contoh diagram Venn
Misalkan A adalah himpunan semua bilangan ganjil yang lebih dari 1 dan kurang dari 8 dengan
himpunan semesta S, maka gambar diagram venn adalah sebagai berikut.

G. Operasi Himpunan

1. Irisan ( ∩ )

Irisan himpunan A dan B adalah himpunan semua anggota semesta yang merupakan  anggota himpunan A dan himpunan B.

A ∩ B = { x| x ∈A   dan x ∈B  }
Jika " X∩Y = ∅ dan Y∩X = ∅ disebut bahwa himpunan X saling lepas dengan himpunan
Y.

Sifat
Misalkan A dan B adalah dua himpunan. Jika  A⊂B , maka  A∩B  = A

2. Gabungan (∪)

Misalkan S adalah himpunan semesta. Gabungan himpunan Adan B adalah himpunan yang
anggotanya semua anggota S yang merupakan anggota himpunan A atau anggota

himpunan
B, dilambangkan dengan ∪
∪ = {x |  x∈A   atau  x∈B  }
Sifat

•  Untuk A dan B himpunan berlaku: n( A∪B ) = n( A ) + n( B ) − n(A∩B )
•  Misalkan A, B dan C adalah himpunan. n( A∪B∪C) = n(A) + n(B) + n(C) −

n( A∩B ) − n(A ∩ C) − n(B ∩ C) + n( A∩B∩C)

3. Komplemen (Complement)

Misalkan S adalah himpunan semesta dan A adalah suatu himpunan. Komplemen
himpunan A adalah suatu himpunan semua anggota himpunan S yang bukan anggota
himpunan A, dilambangkan dengan 
 = {x |  x∈ Sdan    x∉ A}
Hukum de Morgan

4. Selisih (difference)

Definisi
Komplemen relatif B terhadap A adalah himpunan semua anggota himpunan A yang
bukan anggota himpunan B, dilambangkan A− B
A − B   = { x|  x∈A   dan  x∉B  } = 
Sifat
Untuk sebarang himpunan A dan B, berlaku
 Jika A∩B  = ∅, maka A−B = A   dan B−A = B
 Jika A⊂B  , maka A−B   = ∅

SUMBER